北海道高等学校理科研究会「北海道の理科　No.64」(2021)　原稿のhtml版

電流が磁場から受ける力の式　　のあやしげな導出について

１． はじめに

　電流導線が磁場から受ける力−−−フレミングの左手の法則として一括されることも多い，以下本稿では電磁力と呼ぶ−−−の単元を，読者諸氏はどのように教授されているだろうか。実験から入る方法はもちろんあるが，最近，学習者の学習順序に無理のない範囲で理論的に導出が出来ないか試みたところ，ある程度可能であることがわかったので，その方法について紹介する。
　導出にあたり，以下の項目を学習者の既習事項とする¹⁾。

・磁気力に関するクーロンの法則

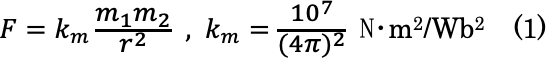
・磁場Hの定義

・直線電流がつくる磁場

・円形一巻き電流が円の中心につくる磁場

　なお，真空の透磁率 は教科書では電磁力の次に登場する物理量¹⁾であるが，式の表現を簡潔にするため，本稿ではこれを含めて導出とする。


２． ビオ・サバールの法則を使う方法

　上に書いた前提と矛盾しているようで恐縮だが，読者諸氏の中には，ビオ・サバールの法則の一部を生徒に話題提供されている方もいらっしゃるのではないだろうか。その場合は，後で述べる第２の方法よりもやや一般的な導出が出来る。

　電流導線の途中の任意の位置に点Pをとる。点Pを含む電流素片をIdsとおく。点Pから距離r[m]離れた点Qにm[Wb]の磁極が置かれているとする。ただし，PQの向きとIdsの向きは互いに垂直とする。（図１）






　電流素片Idsが点Qにつくる微小磁場の大きさをdH_Qとおくと，ビオ・サバールの法則により，



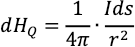
である。したがって，点Qに置かれた磁極mがこの磁場から受ける微小な力の大きさをdF_Qとおくと，(2)より，



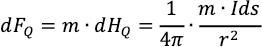
となる。
　次に，点Qに置かれた磁極mが点Pにつくる磁場の大きさをH_Pとおく。(1),(2) より，



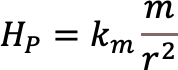
　一方，電流素片Idsにはたらく微小な力の大きさをdF_Pとおく。作用反作用の法則が成り立つと考えるとdF_P = dF_Q 。したがって，



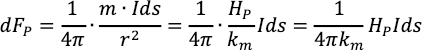
dF_Pは，I,H_P,dsに比例している。そこで，注目している導線の長さをdsのかわりに と書き,またdF_P，H_Pを単にF，Hと書くと，次の式になる。



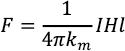
　最後に N/A²とおけば，


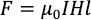
を得る。以上，導出終わり。



３． ビオ・サバールの法則を使わない方法

　ビオ・サバールの法則は，学習指導要領の範囲を超えるので，これを用いて証明するのは本来反則技である。そこで，ビオ・サバールの法則を用いない第２の導出を示そうと思う。

　半径r[m]の円形一巻きの導線に大きさI[A]の電流を流す。（図２）







　円の中心における磁場の大きさをH_oとおく。(4)より，


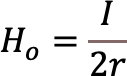
　ここにm[Wb]の磁極をおくときこの磁極にはたらく力の大きさをF_oとおく。(2)より，



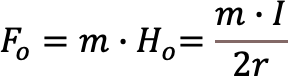
　次に，点Ｏに置いた磁極が導線の場所につくる磁場の大きさをH[N/Wb]とおく。(1),(2)より，



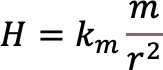
　磁極にはたらく力と円形電流導線の全体にはたらく力の間には作用反作用の法則が成り立つと考える。今，導線の長さ [m]あたりにはたらく力の大きさをFとおく。すると，上に述べた作用反作用の法則により 。したがって，



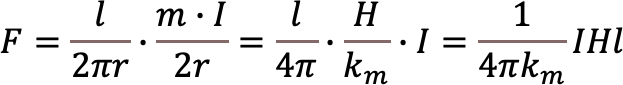
　ここで N/A²とおけば，


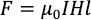
を得る。以上，導出終わり。



４． どこがあやしげなのか

　上に書いた２つの導出は，どちらも，電流導線と磁極の間にはたらく力が作用反作用の法則を満たすことを前提としている。しかし，作用と反作用であれば同一直線上になければならないのに，本導出ではそうなっていない。この点を疑問に思う生徒もいるだろう。これが本稿表題に“あやしげ”と書いた理由である。

　筆者は，矛盾の原因は「磁極」の仮定にあるのではないかと考えている。すなわち，「磁極」を「電流ループ」に置き換えれば矛盾は解消するのではないだろうか。厳密な証明は宿題である。

　磁気の単元が「磁極に対するクーロンの法則」から始まる教科書は多い。その“流れに沿って”電磁力の式を導出してみた。いかがだろうか。


引用文献
1) 国友正和，他「改訂版　物理」数研出版，2017